Fast and Slow Pointer Algorithm: Understanding Cycle Detection in Linked Lists

The fast and slow pointer algorithm is a well-known technique used to detect cycles in data structures like linked lists. It works by having two pointers—one moving at a slower pace and the other moving faster—traverse the list at different speeds. This is an elegant and efficient solution to a common problem, and it’s widely used in many algorithms. In this article, we’ll discuss how the algorithm works, how to implement it in Python, and dive into a mathematical analysis of why it works.

The Cycle Detection Algorithm

Consider a simple Linked List with a potential cycle. In this algorithm, we employ two pointers: slow and fast. Both pointers initially point to the root (head) of the linked list. The key idea is that the slow pointer advances by one node at a time, while the fast pointer moves by two nodes at a time.

• If there is a cycle in the list, the two pointers will eventually meet within the cycle.
• If there’s no cycle, the fast pointer will reach the end of the list and the algorithm concludes that there is no cycle.

The Code

Here’s a simple Python implementation of the linked list and the cycle detection using the fast and slow pointer approach:

from typing import Optional

class Node:
   def __init__(self, data: int) -> None:
      self.data: int = data
      self.next: Optional[Node] = None

class LinkedList:
   def __init__(self) -> None:
      self.root: Optional[Node] = None

   def insert(self, data: int) -> None:
      ''' Insert a node at the end of the list with the given data. '''
      if self.root is None:
         self.root = Node(data)
         return

      node = self.root
      while node.next is not None:
         node = node.next

      node.next = Node(data)

   def find(self, data) -> Optional[Node]:
      ''' Find a node containing the specified data, or return None. '''
      node = self.root
      while node:
         if node.data == data:
            return node
         node = node.next
      return None

   def hasCycles(self) -> bool:
      """Detect if the linked list has a cycle."""
      # Check for edge cases (0 or 1 node)
      if not self.root or not self.root.next:
         return False
      elif self.root == self.root.next:
         return True

      slow = fast = self.root
      while fast and fast.next:
         slow = slow.next
         fast = fast.next.next

         if slow == fast:
            return True

      return False

   def __repr__(self) -> str:
      """Return a string representation of the linked list."""
      nodes = []
      node = self.root
      seen = {}
      while node:
         nodes.append(str(node.data))
         if seen.get(node) is True:
            # We have a cycle, break
            break
         seen[node] = True
         node = node.next

      return " -> ".join(nodes)

How It Works

1. Initialization: Both the slow and fast pointers are initialized to point to the head of the linked list.
2. Traversal: The slow pointer moves one step at a time, while the fast pointer moves two steps at a time.
3. Cycle Detection: If the fast pointer ever equals the slow pointer, we know there is a cycle. If the fast pointer reaches the end of the list (i.e., fast or fast.next is None), then the list doesn’t have a cycle.

Example

Let’s create a linked list, insert some values, and check for a cycle:

# Create a linked list and insert some elements
alist = LinkedList()

for ele in [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]:
    alist.insert(ele)

# Detect if there is a cycle
print(alist.hasCycles())  # Output: False

# Create a cycle
alist.find(10).next = alist.find(2)

# Now the list looks like:
# 1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7 -> 8 -> 9 -> 10
#      ^                                       |
#      |_______________________________________|

print(alist.hasCycles())  # Output: True

Key Questions in Cycle Detection

While the fast and slow pointer algorithm is conceptually simple, it raises several important questions:

1. Why do the fast and slow pointers meet? Is there a case where they don’t meet?
2. If they meet, where do they meet in the cycle?
3. Can we make the cycle detection algorithm faster by increasing the speed of the fast pointer?

Why Do the Pointers Meet?

When there is a cycle, the fast pointer moves at twice the speed of the slow pointer. Intuitively, the fast pointer “laps” the slow pointer and eventually catches up with it. But why does this happen? Let’s break it down mathematically.

Mathematical Analysis of Cycle Detection

Let’s assume that the linked list has a cycle, and the cycle starts after X nodes. The total length of the cycle is Y + Z, where:

• Y is the number of nodes the slow pointer travels before it enters the loop.
• Z is the length of the remaining cycle.

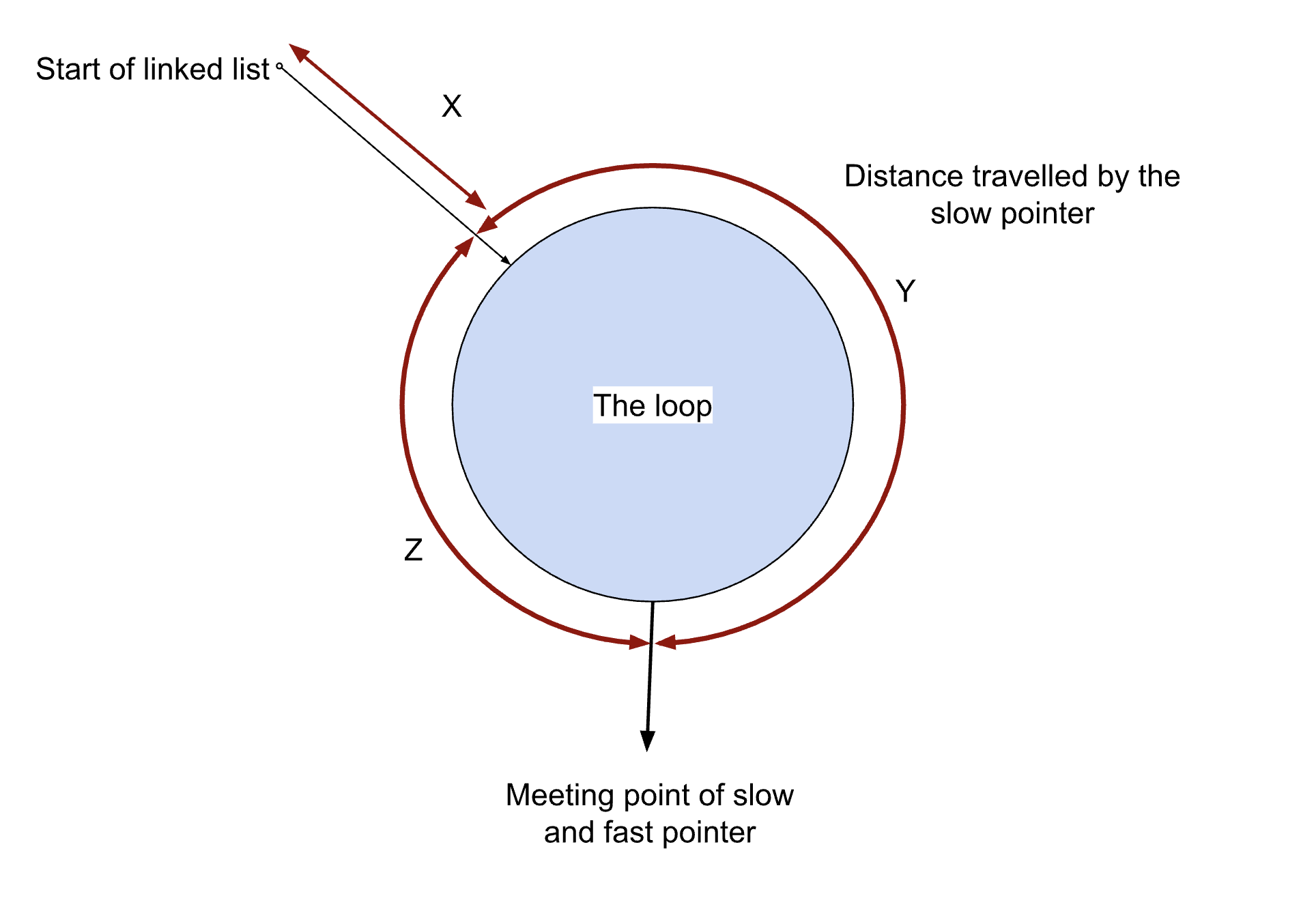When the slow pointer has moved X + Y nodes, the fast pointer has traveled X + (Y + Z) + Y nodes, as it covers the cycle twice as fast.

Using this equation:

(X + (Y + Z) + Y) / 2 = X + Y

Simplifying:

X + (Y + Z) + Y = 2X + 2Y

And:

Y + Z = X + Y
=> Z = X

This means the fast pointer and slow pointer will meet X nodes before the start of the cycle, a crucial observation about the algorithm.

Generalizing the Scenario

Let’s generalize the scenario. Suppose the fast pointer moves k times faster than the slow pointer. In this case, the slow and fast pointers will complete m and n rotations around the loop, respectively, with n > m. To set the stage, assume that when the slow pointer enters the loop, the fast pointer is at some arbitrary position, denoted as i.

As the slow pointer completes one full revolution of the loop in time T = X + Y (where each step takes 1 unit of time), the fast pointer would have traveled k * (X + Y), which corresponds to k full rotations. By this time, the fast pointer will have returned to position i, the same position where it started.

Thus, both pointers would have arrived at their starting position after one full revolution. Therefore, it is reasonable to assume that if they meet during the first revolution of the slow pointer, they will continue to meet at the same point in subsequent revolutions. If they don’t meet during the first revolution, they will never meet at all. Now for the first revolution, let assume the speed of fast pointer is k and fast pointer revolves n times before catching up, we can represent the distance traveled by both pointers as:

Slow pointer: X + Y
Fast pointer: X + n(Y + Z) + Y

After simplifying the equation:

(X + n(Y + Z) + Y) / k = X + Y

Rearranging gives:

(k - 1)X = (n - k + 1)(Y + Z) + (k - 1)Z

Since Y + Z represents the length of the cycle, it can be removed from the equation. The result simplifies to:

(k - 1)X = (k - 1)Z
=> X = Z

Conclusion: The Meeting Point

The key takeaway is that, regardless of how much faster the fast pointer moves compared to the slow pointer (whether 2x, 3x, or k times faster), the slow and fast pointers will always meet at the same point within the first revolution of the slow pointer around the cycle. This means that the time taken for both pointers to meet is same, regardless of the fast pointer’s speed. Ultimately, the meeting point occurs at a distance of X, which is the distance from the start of the linked list to the beginning of the cycle.