Recursion Patterns - Part 2

In the previous post, we explored a foundational recursive pattern for generating sub sequences or the power set of a list by applying a simple “Take or Don’t Take” decision at each element. This backtracking technique serves as a versatile framework for a variety of problems—ranging from generating all subsets, to identifying those that meet a target sum, to handling cases like the Combination Sum problem where elements can be reused. By recursively constructing combinations through inclusion and exclusion, we establish a powerful and reusable template for solving many recursive search challenges efficiently. In this post, we’ll continue our exploration by extending and adapting the Take or Don’t Take approach to tackle more complex scenarios.

Combination sum II

We can follow the same approach we explored in the Combination-1 problem discussed in the earlier article, except this time I’ll demonstrate the solution using C++. The key point to watch out for is avoiding the repeated selection of the same element. This leads us to our first brute-force solution, outlined below.

void combinationSum2Impl(const std::vector<int> &candidates, int target,
                         std::vector<int> &currentCombination,
                         std::size_t index,
                         std::set<std::vector<int>> &results) {
  if (target == 0) {
    auto sortedCombination = currentCombination; // copy current combination
    std::sort(sortedCombination.begin(), sortedCombination.end());
    results.insert(std::move(sortedCombination));
    return;
  }

  if (target < 0 || index >= candidates.size()) {
    return;
  }

  // Include candidates[index]
  currentCombination.push_back(candidates[index]);
  combinationSum2Impl(candidates, target - candidates[index],
                      currentCombination, index + 1, results);
  currentCombination.pop_back();

  // Exclude candidates[index]
  combinationSum2Impl(candidates, target, currentCombination, index + 1,
                      results);
}

std::vector<std::vector<int>>
combinationSum2(std::vector<int> &candidates, int target) {
  std::vector<int> currentCombination;
  std::set<std::vector<int>> results;

  combinationSum2Impl(candidates, target, currentCombination,
                      0, results);

  return {results.begin(), results.end()};
}

As you would notice that we are inserting the successful combinations to a set after sorting. This step is essential as we traverse through the array, we discover combinations that are duplicates of what we found earlier e.g. for a array $[10, 1, 2, 7, 6, 1, 5]$ and target sum 8, with our algorithm we will find [1,7] and [7,1] as possible solutions. To remove this we use sorting and “set” in the above implementation as inserting to a set will automatically remove duplicates. The complexity of this code can be said as O( $n * 2^n*log(k)$) where k is the number of unique combinations. This term is resultant of set insertion operation. With redundant solutions generated, this sure is not the most optimal solution. But how do we only generate non-duplicate solutions. Before we go there let me modify this solution and reduce the number of recursion calls by introducing loops as below

void combinationSum2Impl(vector<int>& candidates, int target, 
                         vector<int>& sub, int start,
                         set<vector<int>>& results) {
	if (target == 0) {
		vector<int> sorted = sub;
		sort(sorted.begin(), sorted.end());
		results.insert(sorted);
		return;
	}
	
	for (int i = start; i < candidates.size(); i++) {
		if (candidates[i] > target) {
			continue; // Skip if candidate is too large
		}
		
		sub.push_back(candidates[i]);
		combinationSum2Impl(candidates, target - candidates[i],
                            sub, i + 1, results);
		sub.pop_back();
	}
}

vector<vector<int>> combinationSum2(vector<int>& candidates,
                                    int target) {
	vector<int> sub;
	set<vector<int>> results;
	
	combinationSum2Impl(candidates, target, sub, 0, results);
	return vector<vector<int>>(results.begin(), results.end());
}

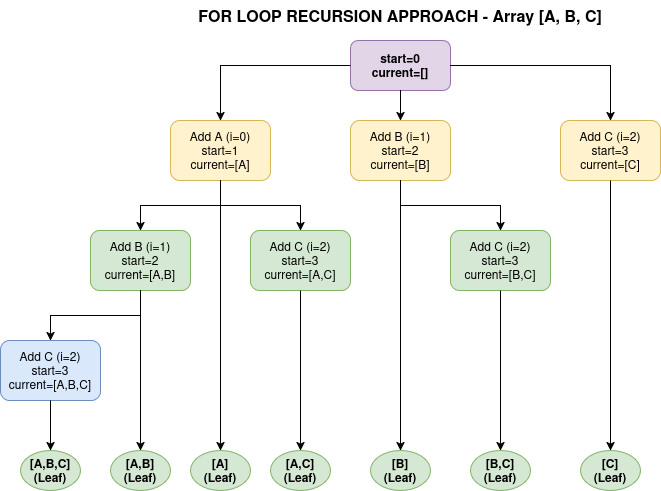
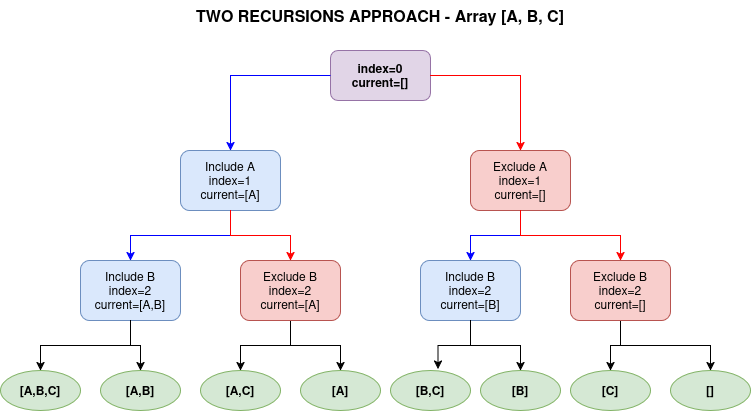
This how the call graph looks like for both for an input $[A,B,C]$ looks like below

You’ll notice that the “for-loop” technique generates incremental and unique combinations progressively, with the amount of work done at each node decreasing the further it is from the starting node. Returning to the original problem, we can optimize the solution further by sorting the input array and skipping over duplicate elements during recursion. This approach also eliminates the need to sort the final sub-sequences or use a set, as only unique combinations will be produced. Below is the final version of the solution.

void combinationSum2Impl(vector<int> &candidates, int target,
                         vector<int> &sub, int start,
                         vector<vector<int>> &results) {
  if (target == 0) {
    results.push_back(sub);
    return;
  }

  for (int i = start; i < candidates.size(); i++) {
    if (candidates[i] > target) {
      break; // Now since the array is sorted, it will only increase
    }

    // The first we have to traverse but after this any duplicates we should
    // avoid.
    if (i != start && candidates[i] == candidates[i - 1]) {
      continue;
    }

    sub.push_back(candidates[i]);
    combinationSum2Impl(candidates, target - candidates[i], sub, i + 1,
                        results);
    sub.pop_back();
  }
}

he 2-way recursion approach generates all possible sub-sequences of the input, effectively constructing the power set. This technique is particularly useful for problems such as:

• Subsets : Generating the complete power set of a given array.
• Subset Sum: Computing and printing all possible subset sums in sorted order.
• Target Sum : The key idea is to either add or subtract the current number at each index. While this problem can be solved recursively, it is inherently a dynamic programming problem and can be further optimized using memoization. Below is a recursive solution.

  int countWays(vector<int>& nums, int i, int sum, int target) {
    if (i == nums.size()) {
        return sum == target ? 1 : 0;
    }
      
    int add = countWays(nums, i + 1, sum + nums[i], target);
    int subtract = countWays(nums, i + 1, sum - nums[i], target);
      
    return add + subtract;
  }
  

• Partition Equal subset Sum : In this problem, we aim to find subsets whose sum equals half of the total sum of the input array. If the total sum is odd, it’s immediately clear that no valid solution exists. Otherwise, we approach the problem similarly to the way we handled the Combination Sum problem discussed earlier.

On the other hand, problems that involve generating combinations with specific constraints often use a “for-loop with one recursion” approach. Examples include:

• Subset II : Generate all unique subsets, similar in structure to Combination Sum II.
• Paliandrome partitioning : The basic recursive approach mirrors Combination Sum II, but instead of checking for a target sum, we verify whether the generated substring is a palindrome. An optimized version of this solution uses dynamic programming.
• Permutations : The core idea resembles Combination Sum II, but here, order matters and each element is used exactly once. A boolean array is used to track which elements have been used. This solution has a time complexity of $O(n! \cdot n)$, since it generates $n!$ permutations. The implementation can be further optimized using element swapping.

void backtrack(const vector<int>& nums, vector<int>& current,
               vector<bool>& used, vector<vector<int>>& result) {
    if (current.size() == nums.size()) {
        result.push_back(current);
        return;
    }

    for (int i = 0; i < nums.size(); i++) {
        if (used[i]) continue;
        used[i] = true;
        current.push_back(nums[i]);

        backtrack(nums, current, used, result);

        current.pop_back();
        used[i] = false;
    }
}

vector<vector<int>> permute(const vector<int>& nums) {
    vector<vector<int>> result;
    vector<int> current;
    vector<bool> used(nums.size(), false);

    backtrack(nums, current, used, result);
    return result;
}

• K-th Permutation : While we could generate all permutations and simply index into the result array to find the answer, this approach has a time complexity of $O(n! \cdot n)$, which is inefficient. Instead, we can take a more mathematical approach. Consider an array like $[1, 2, 3, \dots, n]$. The number of permutations that start with a particular element—say 1—is $(n-1)!$, and the same applies for 2, 3, and so on. This means the $k^\text{th}$ permutation will begin with the element at index $t = k / (n-1)!$. We then remove this element from the array and recursively determine the next element by computing the new index as $k \% (n-1)!$. This continues until we construct the full $k^\text{th}$ permutation.