Recursion Pattern : To Take or Don't Take

Here we will be discussing a recursive template for solving problems related to subsequence generation or power set generation. Generally speaking, this is a variant of the backtracking pattern, where we generate a subsequence out of the input sequence by iterating through each index and deciding whether to “Take” or “Don’t Take” the element at that index.

By definition, a subsequence of a list (or an array) is a sequence that can be derived from another sequence by removing zero or more elements. Thus, we have ( 2^n ) subsequences for a list of ( n ) elements.

For example, the list [1, 2, 3] has the following subsequences:

• [], [1], [2], [3], [1, 2], [1, 3], [2, 3], [1, 2, 3]

---

Let’s dive into this pattern by looking at a problem where we generate all possible subsequences of an array using recursion. The approach is straightforward: each recursive call will “process” the element at a specific index in the array, and then the recursion moves to the next index terminating once we reach end of the array. At each level, we will make two recursive calls for the next level—one where we “Take” the element, and another where we “Don’t Take” the element.

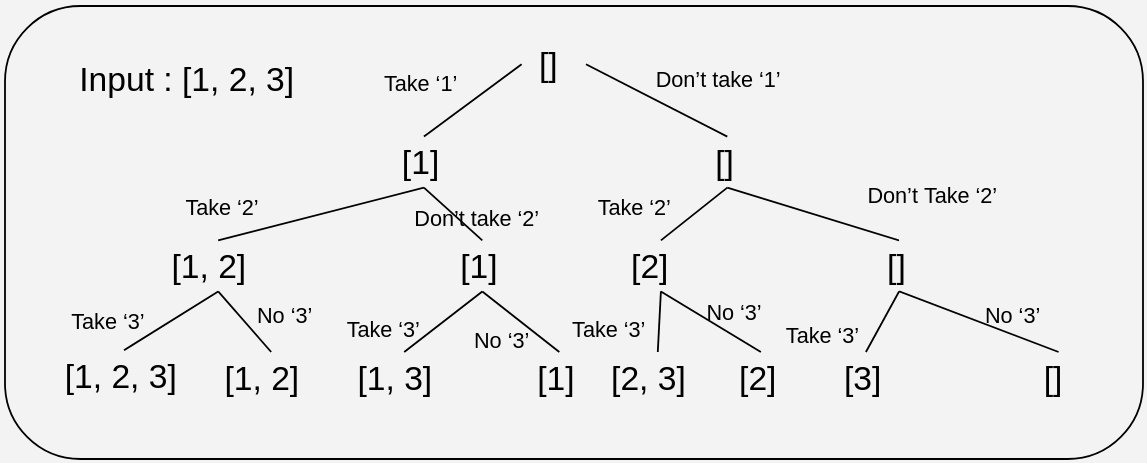
Example: Recursion Tree for Finding Subsequences of [1, 2, 3]

Here’s the recursion tree and code for generating all possible subsequences of the array [1, 2, 3]:

def genSubSequence(source: list, subsequence: list,
                   index: int) -> None:
    # Base case: if we've processed all elements,
    # print the current subsequence
    if index >= len(source):
        print(subsequence)
        return

    # Take the element at the current index
    subsequence.append(source[index])
    genSubSequence(source, subsequence, index + 1)

    # Backtrack by removing the last added element
    # (don't take the element)
    subsequence.pop()

    # Don't take the element at the current index
    genSubSequence(source, subsequence, index + 1)

# Example call
genSubSequence([1, 2, 3], [], 0)

The time complexity of this algorithm is O(( n*2^n )) and spance complexity is O(n).

Similar Problems

The above code demonstrates a generic pattern that can be varied and applied to various problems. Let’s explore some related problems:

---

Problem 1: Print/Count All Subsequences of an Array Which Sum to ‘k’

In the above code, instead of passing the subsequence itself, we pass the sum, which gets incremented with an element at an index if we “take” it, or remains unchanged if we “don’t take” it. This allows us to track the sum of the subsequences as we generate them.

---

Problem 2: Combination Sum

This problem is slightly different from Problem 1 as each element can be picked multiple times. We follow a similar approach to the one in Problem 1, but with a slight modification: when we “take” an element at index i, we do not recurse by incrementing the index. Instead, we reuse the same index, which allows the same element to be picked multiple times.

Here is the code for this approach:

def combinationSumI(source: list, targetSum: int,
                    combination: list, index: int) -> None:
    # Calculate the current sum of the combination
    currSum = sum(combination)

    # Base case: if index is out of range or current sum
    # exceeds target, return
    if index >= len(source) or currSum > targetSum:
        return

    # If we reach the target sum, print the combination
    if currSum == targetSum:
        print(combination)
        return

    # Include the current element and recurse
    combination.append(source[index])
    combinationSumI(source, targetSum, combination, index)

    # Backtrack: remove the last element
    combination.pop()

    # Don't take the element at the current index and move
    # to the next index
    combinationSumI(source, targetSum, combination,
                    index + 1)

# Example call
combinationSumI([2, 3, 5], 8, [], 0)